三角関数

光、音、交流電源、電波、私たちの生活に欠かせないこれらは全て波です。
その波を表すのが三角関数です。

数学の授業では苦しめられる人も少なくない、
でも非常に重要な三角関数について
手を動かしながら理解できたらと思います。

三角関数を構成する3パラメータ

三角関数は振幅、周期(振動数)、位相の3つで表現できます。
　A sin(ft - Φ)
ここでtは変数です。xで表記されることもあると思うので頭の中で置き換えても大丈夫です。
それでは各パラメータの解説です。

振幅

　A sin(ft - Φ)
振幅は波の高さを表します。

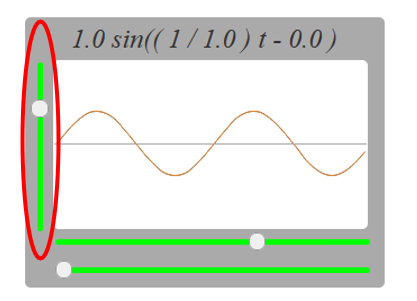
こちらの部分を動かしてみると波の高さが変わります。

Aの値が-1になるとちょうど元の波と上下反対になります。
このようにして波の高さを設定しているのが振幅です。

周期(振動数)

　A sin(ft - Φ)
周期(振動数)は波の幅を表します。
周期と振動数は逆数の関係にあります。周期が10なら振動数は1/10の形ですね。
これらが良くわからない場合、このようなイメージでいてください。
　周期 : 波が1回で何秒か
　周波数 : 1秒間に波が何回上下するか

こちらの部分を動かしてみると周期が変わります。
※左端まで寄せると変なグラフになってしまいます。

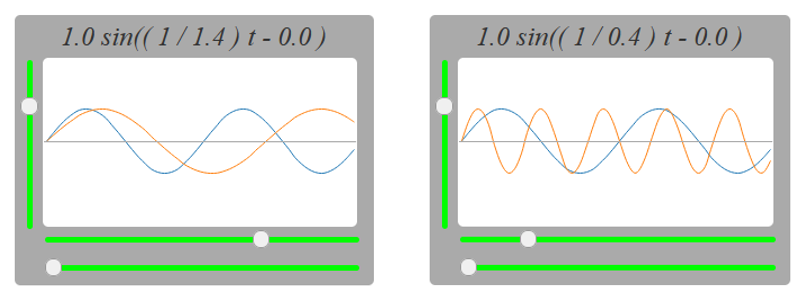
ばねを伸ばしたり縮めたりして横からみるとこうなりますね。

位相

　A sin(ft - Φ)
位相は波を横にスライドさせるものだと思ってください。

こちらの部分を動かしてみると位相が変わります。

山が右にずれていきます。

まとめ

三角関数というのはこれら3つのパラメータの組み合わせです。
世の中にはこんなきれいな形の波ばかりじゃないと思います。
その複雑な波はきれいな波を何種類も重ねて作られるものなんです。
詳しく知りたい方はヨビノリさんの動画をどうぞ！

おまけ

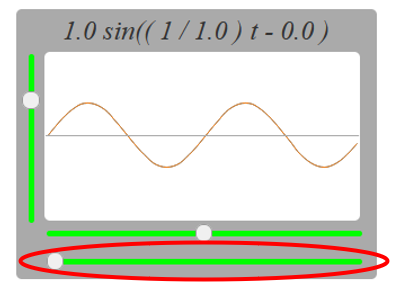
周期のパラメータを左に寄せると・・・。

解説は準備中です。